Abstract
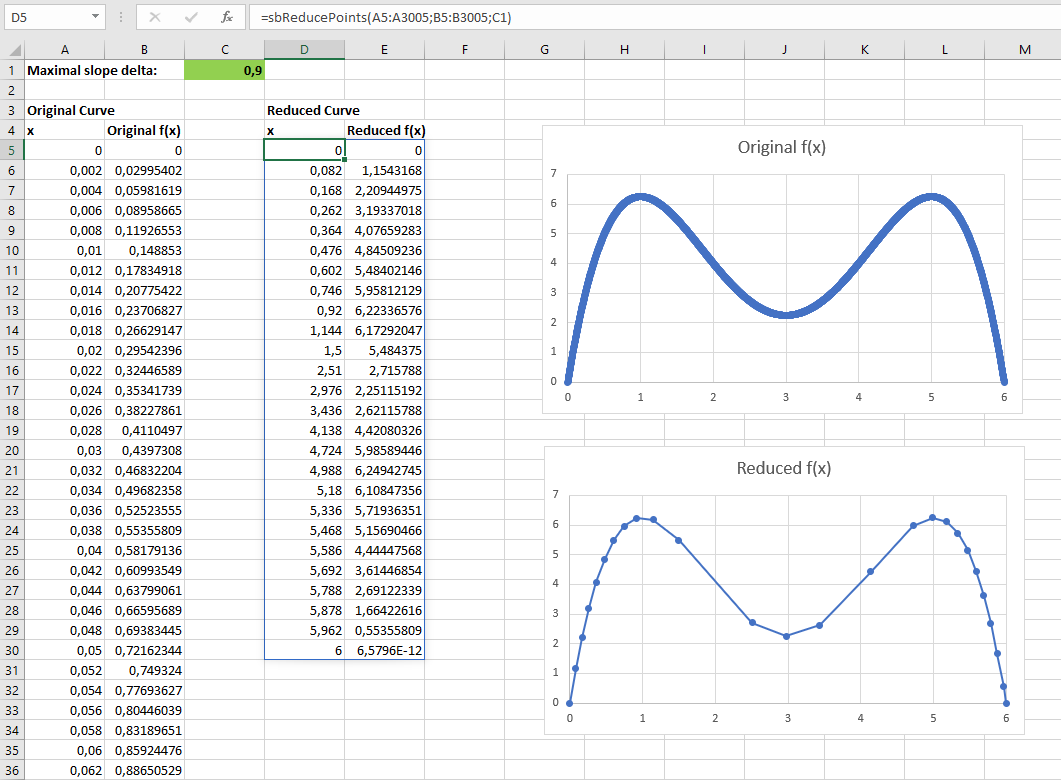
If you need to reduce the number of curve points to those only showing a significant slope change:
Literature
If this simple slope change approach is not successful, use the (external link!) Ramer–Douglas–Peucker algorithm.
Appendix sbReducePoints Code
Please read my Disclaimer.
Option Explicit
Function sbReducePoints(rX As Range, rY As Range, _
Optional dMaxSlopeDelta As Double = 0.001) As Variant
'sbReducePoints eliminates points from a given set
'in case the slopes between these points do not differ
'too much.
'Source (EN): http://www.sulprobil.de/sbreducepoints_en/
'Source (DE): http://www.berndplumhoff.de/sbreducepoints_de/
'(C) (P) by Bernd Plumhoff 29-Mar-2023 PB V0.1
Dim bNewSlope As Boolean
Dim dSlope12 As Double
Dim dSlope13 As Double
Dim dSlope23 As Double
Dim i As Long
Dim k As Long
Dim lcount As Long
With Application.WorksheetFunction
lcount = rX.Rows.Count
If rX.Columns.Count > lcount Then
lcount = rX.Columns.Count
End If
ReDim dX(1 To lcount) As Double
ReDim dY(1 To lcount) As Double
'read data row-wise or column-wise
If rX.Rows.Count > rX.Columns.Count Then
For i = 1 To lcount
dX(i) = rX.Cells(i, 1)
dY(i) = rY.Cells(i, 1)
Next i
Else
For i = 1 To lcount
dX(i) = rX.Cells(1, i)
dY(i) = rY.Cells(1, i)
Next i
End If
ReDim vR(1 To 2, 1 To lcount) As Variant
vR(1, 1) = dX(1)
vR(2, 1) = dY(1)
vR(1, 2) = dX(2)
vR(2, 2) = dY(2)
k = 2
bNewSlope = True
For i = 3 To lcount
If bNewSlope Then dSlope12 = (vR(2, k) - vR(2, k - 1)) / (vR(1, k) - vR(1, k - 1))
dSlope13 = (dY(i) - vR(2, k - 1)) / (dX(i) - vR(1, k - 1))
dSlope23 = (dY(i) - vR(2, k)) / (dX(i) - vR(1, k))
If Abs(dSlope13 - dSlope12) > dMaxSlopeDelta Or _
Abs(dSlope13 - dSlope23) > dMaxSlopeDelta Then
k = k + 1
bNewSlope = True
Else
bNewSlope = False
End If
vR(1, k) = dX(i)
vR(2, k) = dY(i)
Next i
ReDim Preserve vR(1 To 2, 1 To k) As Variant
If rX.Rows.Count > rX.Columns.Count Then
sbReducePoints = .Transpose(vR)
Else
sbReducePoints = vR
End If
End With
End Function
Please read my Disclaimer.
sbReducePoints.xlsm [192 KB Excel file, open and use at your own risk]