Abstract
Let us assume you have three different products, each of them with three different types with different weights, of which you have different amounts. Of product PR you have 7 pieces of weight 404 g, then you have 4 pieces of weight 401 g, and 5 pieces with 398 g. In addition to that you have similar products BB and BO:
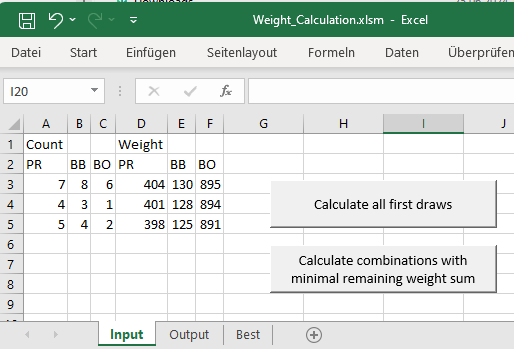
Now you need to determine 3 by 3 products (each product appearing exactly once, but types can occur more than once) with identical weight sums:
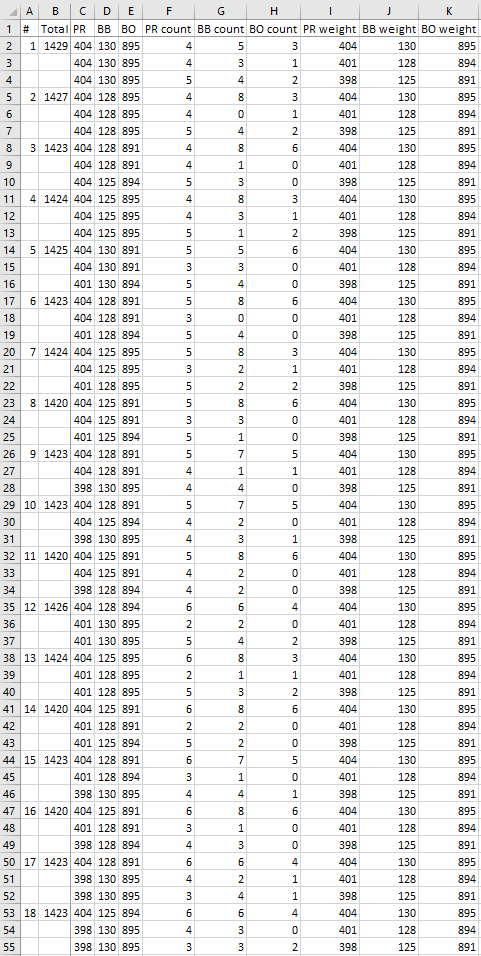
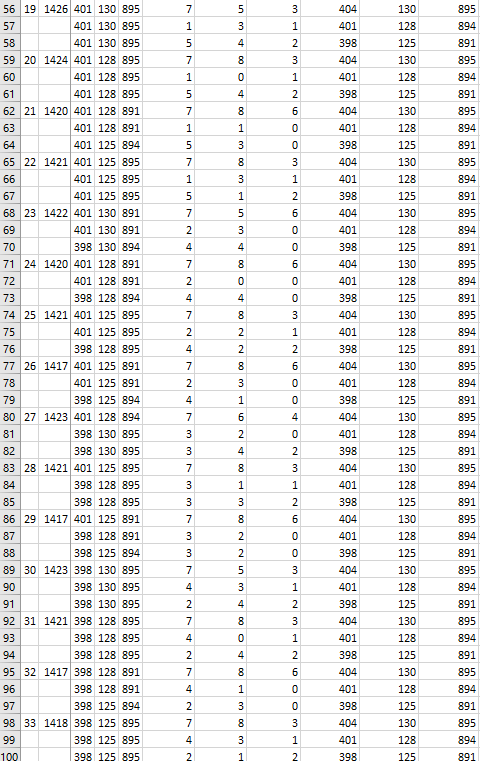
There are many options to calculate alle possible draws. The appendix shows a very simple but costly option (see first download file) which naivly traverses through all possible combinations. The second download file offers a Monte Carlo simulation which uses the function UniqRandInt UniqRandInt to very likely (but not surely) identify all possibilities with 500,000 iterations. A third option would be making use of the function combinations_with_k_subsets_of_n to check all possible 84 * 84 * 20 = 141,120 permutations.
One combination (there are 12 of them) of subsequent draws with the smallest remaining sum of weights is:
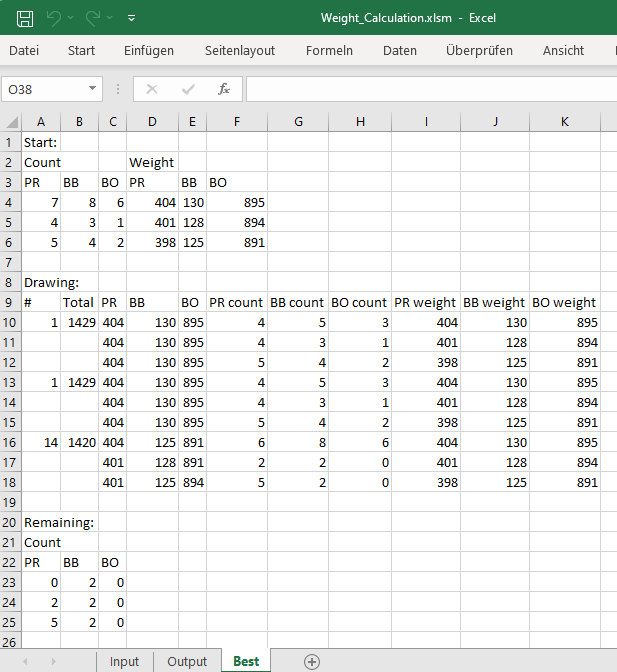
All 12 different draw combinations - numbers specify the output variant listed above:
| First Draw | Second Draw | Third Draw |
|---|---|---|
| 1 | 1 | 14 |
| 1 | 1 | 16 |
| 1 | 1 | 21 |
| 1 | 1 | 24 |
| 1 | 2 | 23 |
| 1 | 3 | 19 |
| 1 | 5 | 7 |
| 1 | 5 | 13 |
| 1 | 5 | 20 |
| 1 | 6 | 19 |
| 1 | 9 | 12 |
| 2 | 5 | 19 |
Appendix – AllFirstDraws and CombinationsWithMinRemainingWeight Code
Please read my Disclaimer.
Option Explicit
'Calculates 3 * 3 - tuples of same total weights.
'Source (EN): https://www.sulprobil.de/weight_calculation_en/
'Source (DE): https://www.berndplumhoff.de/gewichtberechnung_de/
'(C) (P) by Bernd Plumhoff 26-Jun-2024 PB V0.4
Sub AllFirstDraws()
Dim i As Long
Dim j As Long
Dim k As Long
Dim i2 As Long
Dim j2 As Long
Dim k2 As Long
Dim i3 As Long
Dim j3 As Long
Dim k3 As Long
Dim m As Long
Dim n As Long
Dim t As Long
Dim v As Long
Dim oGetRidofDupes As Object
Dim vCount As Variant
Dim vWeight As Variant
Dim state As SystemState
With Application.WorksheetFunction
Set state = New SystemState
wsI.Cells.EntireColumn.AutoFit
wsO.Cells.ClearContents
Set oGetRidofDupes = CreateObject("Scripting.Dictionary")
i = 1
Do While wsI.Cells(2, i) <> ""
i = i + 1
Loop
n = (i - 1) \ 2
vCount = .Transpose(Range(wsI.Cells(3, 1), wsI.Cells(3, n).End(xlDown)))
vWeight = .Transpose(Range(wsI.Cells(3, n + 1), wsI.Cells(3, 2 * n).End(xlDown)))
For i = 1 To n
k = 0
For j = 1 To UBound(vCount, 2)
k = k + vCount(j, i)
Next j
If k < n Then
Call MsgBox("Not enough items in column " & i, vbOKOnly, "Error")
Exit Sub
End If
Next i
m = j - 1
'Debug.Print "n = " & n, "m = " & m
'Now we know the dimensions
ReDim sItem(1 To n) As String
wsO.Cells(1, 1) = "#"
wsO.Cells(1, 2) = "Total"
For i = 1 To n
sItem(i) = wsI.Cells(2, i)
wsO.Cells(1, i + 2) = sItem(i)
wsO.Cells(1, n + 2 + i) = sItem(i) & " count"
wsO.Cells(1, 2 * n + 2 + i) = sItem(i) & " weight"
Next i
ReDim lPermutWeight(1 To n, 1 To n * m) As Long
ReDim lPermutIdx(1 To n) As Long
ReDim lPermutSubGroupIdx(1 To n, 1 To n * m) As Long
For i = 1 To n
t = 0
For j = 1 To m
For k = 1 To .Min(n, vCount(i, j))
t = t + 1
lPermutWeight(i, t) = vWeight(i, j)
lPermutSubGroupIdx(i, t) = j
Next k
Next j
lPermutIdx(i) = t
Next i
v = 2
For i = 1 To lPermutIdx(1)
For j = 1 To lPermutIdx(1)
If j <> i Then
For k = 1 To lPermutIdx(1)
If k <> j And k <> i Then
For i2 = 1 To lPermutIdx(2)
For j2 = 1 To lPermutIdx(2)
If j2 <> i2 Then
For k2 = 1 To lPermutIdx(2)
If k2 <> j2 And k2 <> i2 Then
For i3 = 1 To lPermutIdx(3)
For j3 = 1 To lPermutIdx(3)
If j3 <> i3 Then
For k3 = 1 To lPermutIdx(3)
If k3 <> j3 And k3 <> i3 Then
'Debug.Print lPermutWeight(1, i) & " + " & lPermutWeight(2, i2) & " + " & lPermutWeight(3, i3) & " ?= " & lPermutWeight(1, j) & " + " & lPermutWeight(2, j2) & " + " & lPermutWeight(3, j3) & " And " & lPermutWeight(1, i) & " + " & lPermutWeight(2, i2) & " + " & lPermutWeight(3, i3) & " ?= " & lPermutWeight(1, k) & " + " & lPermutWeight(2, k2) & " + " & lPermutWeight(3, k3)
If lPermutWeight(1, i) + lPermutWeight(2, i2) + lPermutWeight(3, i3) = _
lPermutWeight(1, j) + lPermutWeight(2, j2) + lPermutWeight(3, j3) And _
lPermutWeight(1, i) + lPermutWeight(2, i2) + lPermutWeight(3, i3) = _
lPermutWeight(1, k) + lPermutWeight(2, k2) + lPermutWeight(3, k3) Then
If Not oGetRidofDupes.exists(lPermutWeight(1, i) & "|" & lPermutWeight(2, i2) & "|" & lPermutWeight(3, i3) & "|" & _
lPermutWeight(1, j) & "|" & lPermutWeight(2, j2) & "|" & lPermutWeight(3, j3) & "|" & _
lPermutWeight(1, k) & "|" & lPermutWeight(2, k2) & "|" & lPermutWeight(3, k3)) Then
oGetRidofDupes(lPermutWeight(1, i) & "|" & lPermutWeight(2, i2) & "|" & lPermutWeight(3, i3) & "|" & _
lPermutWeight(1, j) & "|" & lPermutWeight(2, j2) & "|" & lPermutWeight(3, j3) & "|" & _
lPermutWeight(1, k) & "|" & lPermutWeight(2, k2) & "|" & lPermutWeight(3, k3)) = 1
oGetRidofDupes(lPermutWeight(1, i) & "|" & lPermutWeight(2, i2) & "|" & lPermutWeight(3, i3) & "|" & _
lPermutWeight(1, k) & "|" & lPermutWeight(2, k2) & "|" & lPermutWeight(3, k3) & "|" & _
lPermutWeight(1, j) & "|" & lPermutWeight(2, j2) & "|" & lPermutWeight(3, j3)) = 1
oGetRidofDupes(lPermutWeight(1, j) & "|" & lPermutWeight(2, j2) & "|" & lPermutWeight(3, j3) & "|" & _
lPermutWeight(1, i) & "|" & lPermutWeight(2, i2) & "|" & lPermutWeight(3, i3) & "|" & _
lPermutWeight(1, k) & "|" & lPermutWeight(2, k2) & "|" & lPermutWeight(3, k3)) = 1
oGetRidofDupes(lPermutWeight(1, j) & "|" & lPermutWeight(2, j2) & "|" & lPermutWeight(3, j3) & "|" & _
lPermutWeight(1, k) & "|" & lPermutWeight(2, k2) & "|" & lPermutWeight(3, k3) & "|" & _
lPermutWeight(1, i) & "|" & lPermutWeight(2, i2) & "|" & lPermutWeight(3, i3)) = 1
oGetRidofDupes(lPermutWeight(1, k) & "|" & lPermutWeight(2, k2) & "|" & lPermutWeight(3, k3) & "|" & _
lPermutWeight(1, i) & "|" & lPermutWeight(2, i2) & "|" & lPermutWeight(3, i3) & "|" & _
lPermutWeight(1, j) & "|" & lPermutWeight(2, j2) & "|" & lPermutWeight(3, j3)) = 1
oGetRidofDupes(lPermutWeight(1, k) & "|" & lPermutWeight(2, k2) & "|" & lPermutWeight(3, k3) & "|" & _
lPermutWeight(1, j) & "|" & lPermutWeight(2, j2) & "|" & lPermutWeight(3, j3) & "|" & _
lPermutWeight(1, i) & "|" & lPermutWeight(2, i2) & "|" & lPermutWeight(3, i3)) = 1
wsO.Cells(v, 1) = (v + 1) \ n
wsO.Cells(v, 2) = lPermutWeight(1, i) + lPermutWeight(2, i2) + lPermutWeight(3, i3)
wsO.Cells(v, 3) = lPermutWeight(1, i)
wsO.Cells(v, 4) = lPermutWeight(2, i2)
wsO.Cells(v, 5) = lPermutWeight(3, i3)
wsO.Cells(v + 1, 3) = lPermutWeight(1, j)
wsO.Cells(v + 1, 4) = lPermutWeight(2, j2)
wsO.Cells(v + 1, 5) = lPermutWeight(3, j3)
wsO.Cells(v + 2, 3) = lPermutWeight(1, k)
wsO.Cells(v + 2, 4) = lPermutWeight(2, k2)
wsO.Cells(v + 2, 5) = lPermutWeight(3, k3)
wsO.Cells(v, 6) = vCount(1, 1) - IIf(lPermutSubGroupIdx(1, i) = 1, 1, 0) - IIf(lPermutSubGroupIdx(1, j) = 1, 1, 0) - IIf(lPermutSubGroupIdx(1, k) = 1, 1, 0)
wsO.Cells(v, 7) = vCount(2, 1) - IIf(lPermutSubGroupIdx(2, i2) = 1, 1, 0) - IIf(lPermutSubGroupIdx(2, j2) = 1, 1, 0) - IIf(lPermutSubGroupIdx(2, k2) = 1, 1, 0)
wsO.Cells(v, 8) = vCount(3, 1) - IIf(lPermutSubGroupIdx(3, i3) = 1, 1, 0) - IIf(lPermutSubGroupIdx(3, j3) = 1, 1, 0) - IIf(lPermutSubGroupIdx(3, k3) = 1, 1, 0)
wsO.Cells(v + 1, 6) = vCount(1, 2) - IIf(lPermutSubGroupIdx(1, i) = 2, 1, 0) - IIf(lPermutSubGroupIdx(1, j) = 2, 1, 0) - IIf(lPermutSubGroupIdx(1, k) = 2, 1, 0)
wsO.Cells(v + 1, 7) = vCount(2, 2) - IIf(lPermutSubGroupIdx(2, i2) = 2, 1, 0) - IIf(lPermutSubGroupIdx(2, j2) = 2, 1, 0) - IIf(lPermutSubGroupIdx(2, k2) = 2, 1, 0)
wsO.Cells(v + 1, 8) = vCount(3, 2) - IIf(lPermutSubGroupIdx(3, i3) = 2, 1, 0) - IIf(lPermutSubGroupIdx(3, j3) = 2, 1, 0) - IIf(lPermutSubGroupIdx(3, k3) = 2, 1, 0)
wsO.Cells(v + 2, 6) = vCount(1, 3) - IIf(lPermutSubGroupIdx(1, i) = 3, 1, 0) - IIf(lPermutSubGroupIdx(1, j) = 3, 1, 0) - IIf(lPermutSubGroupIdx(1, k) = 3, 1, 0)
wsO.Cells(v + 2, 7) = vCount(2, 3) - IIf(lPermutSubGroupIdx(2, i2) = 3, 1, 0) - IIf(lPermutSubGroupIdx(2, j2) = 3, 1, 0) - IIf(lPermutSubGroupIdx(2, k2) = 3, 1, 0)
wsO.Cells(v + 2, 8) = vCount(3, 3) - IIf(lPermutSubGroupIdx(3, i3) = 3, 1, 0) - IIf(lPermutSubGroupIdx(3, j3) = 3, 1, 0) - IIf(lPermutSubGroupIdx(3, k3) = 3, 1, 0)
wsO.Cells(v, 9) = vWeight(1, 1)
wsO.Cells(v, 10) = vWeight(2, 1)
wsO.Cells(v, 11) = vWeight(3, 1)
wsO.Cells(v + 1, 9) = vWeight(1, 2)
wsO.Cells(v + 1, 10) = vWeight(2, 2)
wsO.Cells(v + 1, 11) = vWeight(3, 2)
wsO.Cells(v + 2, 9) = vWeight(1, 3)
wsO.Cells(v + 2, 10) = vWeight(2, 3)
wsO.Cells(v + 2, 11) = vWeight(3, 3)
v = v + 3
End If
End If
End If
Next k3
End If
Next j3
Next i3
End If
Next k2
End If
Next j2
Next i2
End If
Next k
End If
Next j
Next i
wsO.Cells.EntireColumn.AutoFit
End With
End Sub
Sub CombinationsWithMinRemainingWeight()
Dim i As Long
Dim j As Long
Dim k As Long
Dim m As Long
Dim maxsum As Long
Dim n As Long
Dim sum(1 To 33) As Long
Dim t As Long
Dim u As Long
Dim v As Long
Dim w As Long
Dim vCount As Variant
Dim vC(1 To 33) As Variant
Dim vCi(1 To 3) As Variant
Dim state As SystemState
With Application.WorksheetFunction
Set state = New SystemState
i = 1
Do While wsI.Cells(2, i) <> ""
i = i + 1
Loop
n = (i - 1) \ 2
vCount = .Transpose(.Transpose(Range(wsI.Cells(3, 1), wsI.Cells(3, n).End(xlDown))))
For i = 1 To n
k = 0
For j = 1 To UBound(vCount, 2)
k = k + vCount(j, i)
Next j
If k < n Then
Call MsgBox("Not enough items in column " & i, vbOKOnly, "Error")
Exit Sub
End If
Next i
m = j - 1
i = 2
t = wsO.Cells(i, 1)
Do While t <> 0
sum(t) = wsO.Cells(i, 2)
vC(t) = .Transpose(.Transpose(Range(wsO.Cells(i, 6), wsO.Cells(i + 2, 8))))
i = i + 3
t = wsO.Cells(i, 1)
Loop
t = 0
maxsum = 0
For i = 1 To 33
vCi(1) = vC(i)
For j = 1 To 33
vCi(2) = vCi(1)
For m = 1 To 3
For n = 1 To 3
If vCi(1)(m, n) < vCount(m, n) - vC(j)(m, n) Then GoTo Label_Next_j
vCi(2)(m, n) = vCi(1)(m, n) - vCount(m, n) + vC(j)(m, n)
Next n
Next m
For k = 1 To 33
vCi(3) = vCi(2)
For m = 1 To 3
For n = 1 To 3
If vCi(2)(m, n) < vCount(m, n) - vC(k)(m, n) Then GoTo Label_Next_k
vCi(3)(m, n) = vCi(2)(m, n) - vCount(m, n) + vC(k)(m, n)
Next n
Next m
If maxsum <= 3 * (sum(i) + sum(j) + sum(k)) Then
maxsum = 3 * (sum(i) + sum(j) + sum(k))
t = t + 1
Debug.Print t, maxsum, i, j, k
End If
Label_Next_k:
Next k
Label_Next_j:
Next j
Next i
End With
End Sub
Useful Extensions and Generalisations
With these approaches the quick and not too clean first solution mentioned above could be extended:
https://stackoverflow.com/questions/54669041/vba-write-all-permutations-of-numbers-to-an-array
(also here: https://www.vitoshacademy.com/vba-nested-loops-with-recursion/ )
https://www.codeproject.com/Tips/759707/Generating-dynamically-nested-loops
https://stackoverflow.com/questions/1737289/dynamic-nested-loops-level
Download
Please read my Disclaimer.
Weight_Calculation.xlsm [50 KB Excel file, open and use at your own risk]
Weight_Calculation_MC.xlsm [58 KB Excel file, open and use at your own risk]